○ 从江县下江中学 何兴健

平面几何是初中数学的入门学科，几何推理证明更是初中数学学习的难点和重点。教师在教学过程中应该让学生掌握正确的解题思路，探讨证明过程中的数学思维，总结证明题证明的技巧规律。笔者结合课题研究有如下体会：

一、培养看图读图能力，树立几何思想

几何证明题最大的特点就是要从题目所给的图形中寻找信息，这就要求学生能够敏锐地发现图形的特点及其中所包含的联系，从而获得解题的思路。同样，最大的难点也是读图，几何证明题的突破口往往隐藏在所给图形中，只有能够从图形中发掘到线索，才能够真正解决几何证明题。

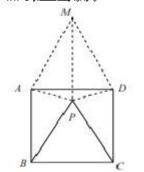
例如，“如图，P 为正方形 ABCD 内 部的一点，∠ PAD ＝∠ PDA ＝ 15°，求 证：△ PBC 是正三角形。”

文字内容比较少，题干中较多的信息包含在图形中，通过作辅助图形，作出△ ADM，连接 MP，由图形的信息可以得知△ APD 为等腰三角形，并且通过推导可以知道△ MAP 与△ MDP全等，并且 AM=AB，∠MAP＝∠BAP＝ 75°，则△ MAP 与△ BAP 全等，所以 MP ＝ AB ＝ AM，进而可以知道△ PBC 各个角均为 60°，故可以证得△ PBC 为正三角形。本题的大多数信息均在图形中提取，教师要重点培养学生挖掘题干中隐藏信息的能力，由角相等可知等腰三角形，正方形可知各个边相等，各个角均为直角，这就给解题提供了方便。若想强化学生几何证明题的能力，就必须提高学生的看图、读图的能力，培养学生逻辑能力和空间想象能力。

二、规范解题分析步骤，规范答题思路

对于几何证明题来说，规范的解题步骤能够体现出学生清晰的思路，教师判断起来也更加便于理解，在具有几何证明题答题思路的同时，还需要写出规范的答题步骤，学生必须要有清晰的思路和很强的逻辑思维，才能够在几何证明的书写过程中发掘几何图形中的解题线索。如果学生在解题时的思路不清晰，那么解题步骤的书写就会很混乱。教师要指导学生在分析出题目中所有的线索之后，引导学生从中提取关键得分点，规范解题步骤并将思路体现在卷面上。教师在几何教学中要紧紧联系课本上的理论知识，作为解答几何问题的基础，这有利于学生在解答书写过程中把握住得分的关键点，体会到几何问题的依据和逻辑性。教师可以在几何证明类题目的专题课堂上书写一道几何证明题的完整解题步骤，并注明评分标准，可以让学生自主总结出几何证明类题目的一般答题步骤，再进行交流，发现其中缺少的关键步骤，也能够加深学生对于解题关键步骤的记忆。同时，结合对几何证明题的实践，能够不断加深学生对于几何学的认识，使几何证明题的解题思路更加清晰，逐渐提高学生的几何逻辑能力。

三、根据结果倒推条件，清晰证明思路

在初中解答几何证明题的时候，如果题目较为混乱，并且图形复杂，这就要求培养学生几何思想中的逆变化思维，从题干中所要证明的部分出发，从反方向进行解题，根据所要证明的内容来推倒所需要的条件，这样能够使解题的思路更加清晰，对于一些学生也更加利于理解，并且能够有效减少解题过程中花费的时间，学生在做起几何证明题时能够得心应手，攻克几何证明题。

例如，要证明两个三角形全等，一般需要提供三个条件才能够完成。运用几何知识分析时要想找出证明全等的条件，然后分析如何得出这些条件，然而在卷面上的书写却恰恰相反。例如，在四边形 ABCD 中，AD＝BC，AE ⊥ BD，CF ⊥ BD，垂足分别为 E、F，BE＝DF，求证：△ ADE ≌△ CBF。首先，学生要具有一定的逻辑思维能力，能够自主想象出图形的形状，按照逆推倒的思路，要证明 △ ADE ≌△ CBF，由题干可知存在两个直角相等，并且AD＝BC，只需要再证DE＝BF 即可，此时解题思路就清晰了，只需要按照规范的解题过程书写下来就可以了。这种通过结果来推倒条件，在几何证明题中能够使学生的思路更加清晰，思维更加顺畅。

在初中平面几何证明题的解题过程中，注重审题能力，根据提干要求灵活运用，将知识点难点重点掌握，懂得解后总结归纳反思，几何证明题这个难点将不再成为难点。