○ 榕江县第三高级中学 白 宁

数学教育须注重学生分析问题和思考问题能力的培养，我们作为一线教师，对这些能力的培养，要注重方式方法。“一题多解”与“一题多变”在我们数学教学中，在培养学生数学思维能力方面越来越受到重视。本文将阐述“一题多解”和“一题多变”在数学学习中的运用，并用例题说明其重要性。

一、高中生对学习数学的认识

从近年高考数学试题来看，学生模拟题中用的所谓的套路不再适应新高考。数学的学习需要知识的不断渗透，应该让学生去经历、感受知识的形成过程，体会其背后的数学思想。万变不离其宗，试题的表征形式千千万，但是知识的本源就是课本上的基本数学概念、公式、定理。

二、推导公式中运用“一题多解”

教学实践证明，熟练地理解并掌握公式，运用公式是最重要的。其实每个公式的推导过程本身就是一种基础的解题方法，或者说是一种解题技巧。如果我们在教学中，在公式的推导过程中经常运用“一题多解”，让学生自己经历知识的形成过程，同时也可以掌握解题基本的规律和方法，达到事半功倍的效果。

例如我们在学习两角和与差余弦公式 时，

方法一：设[~公式~]，

则[~公式~].

在[~公式~]中，

∵[~公式~]，

｀[~公式~]，

｀[~公式~].

这种方法是运用两点间距离公式和余弦定理，两个知识引导学生建立等式关系，是比较容易接受的一种方法。

方法二：

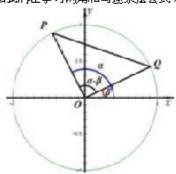
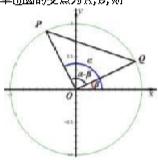
在平面直角坐标系[~公式~]内，如图单位圆[~公式~]，角α，β的终边与单位圆的交点为A，B，则

[~公式~]，[~公式~]

[~公式~][~公式~]=[~公式~][~公式~]

[~公式~]

有[~公式~].

这样运用两种方法推导，体会两角和与差的余弦公式的形成过程，可以对这个过程的印象更深刻、更具体，相比单纯死记硬背公式，更有利于学生思维能力的开发，这样的例子在高中阶段数学学习新课讲授过程中还有很多。

三、在例题讲解中运用“一题多解”和“一题多变”

“一题多变”和“一题多解”在数学学习过程中，可以起到纽带作用。“一题多解”因思考的角度不同从而得到多种不同的思路，对于学生开拓数学的解题思路，提高分析问题的思维能力。“一题多变”是对一道数学题或类比、或联想、或推广，从而得到一系列新的题目，或者得出一些一般性的数学二阶结论，尝试变式题的求解，哪怕是不能解决也好。尝试的过程也有利于学生应变能力的培养，慢慢形成发散思维。

下面例题讲解中“一题多解”和“一题多变”的应用来说明：

例1：[~公式~]的三边[~公式~]满足[~公式~]，求证：[~公式~]。

证法一：由余弦定理，

[~公式~]

又[~公式~]，所以[~公式~]．

证法二：由正弦定理，

[~公式~]

又[~公式~]，

所以[~公式~]，

所以[~公式~]，又[~公式~]，

所以[~公式~]，所以[~公式~]．

例2：已知[~公式~]的内角A，B，C的对边分别为a，b，c，已知[~公式~]（1）求A；（2）若[~公式~]，证明：[~公式~]是直角三角形。母题为2020·全国2卷文科17题

变式练1：若[~公式~]，[~公式~]，求[~公式~]，[~公式~]；

变式练2：若[~公式~]，[~公式~]，求[~公式~]的面积

变式练3： 若[~公式~]，[~公式~]的面积为[~公式~]，求[~公式~]的周长

由一道解三角形的高考母题进行变式训练，让学生经历这个过程，在抓住基础知识的同时，还激发了探索求知的欲望，从而可以更加精准地实现教学的目标和要求。

四、习题中运用“一题多解”和“一题多变”的训练

在数学教学中，我们很多教师经常会给学生布置很多的课外作业，学生也常常感到学习的负担沉重，学生学习数学的兴趣也逐步消失无存。为什么我们不从课本上的经典例题、习题入手，演变，加深呢？这样慢慢坚持学生的解题能力得到逐渐提高，面对从未见过的新题才会有迎刃而解的能力。

通过坚持“一题多解”这一方式，使学生主动思考解答，这样学生的解题思路和技巧慢慢更加熟练了。“一题多变”的坚持练习提高学生对知识的整体认知，逐渐地学生会发现不同类型的题目是有相关性的，从而能根据不同的情况调整思维方法，不陷入固定模式里。

在我们高中数学平时的教学中运用“一题多解”与“一题多变”的教学方法，不仅能提高学生的解题能力，又能培养学生的思维方式。 学生养成高效的学习方法，使其更好地适应新高考，是很有实践意义的。