○ 榕江县第二中学 陆道芬
一、数形结合思想的概念
数形结合思想就是通过数和形之间的对应关系和相互转化来解决问题的思想方法。数学是研究现实世界的数量关系与空间形式的科学,数和形之间是既对立又统一的关系,在一定的条件下可以相互转化。数形结合思想是一种直观的解题方法,思路明确、形式简单、实用性强等特点。用数与形之间的彼此转化去解决实际的数学问题就是数形结合思想的本质所在。不断引导学生用数形结合的方法去思考问题,迅速提高学生对抽象的数学符号语言产生极大的兴趣。即采用“先实践后理论”的教学方法,将理论知识融入实际感受和实践操作中去,使抽象的学习内容具体化,能有效地提高学生的学习效率和积极性。既能让学生学在其中乐在其里,又能培养学生的分析问题的思维能力;把数与形相互结合的思想运用到数学教学课堂逆向教学设计中来更直观、形象地把数学知识具体化;更能让学生感受到数学的奇妙之处,让学生对学习数学产生兴趣。
二、数形结合在部分中学数学课堂中的体现
下面分别从:1.证明恒等式;2.求参数的值或参数的取值范围;3.求最值问题;4.用代数与三角方法解决几何问题,从而使复杂问题简单化,抽象问题具体化。这几个方面进行探讨数形结合在部分中学数学逆向教学中的体现。
1.证明恒等式
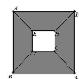
例1 运用数形结合的思维方式对于恒等的证明比直接用代数的方法要形象简单得多。例如给学生讲解勾股定理时,我们可以适当地先提出一些问题,该问题即是学生目前已掌握的,对我要解决的新知识点起到承上启下的作用。让学生学起来才感觉不到陌生,对于知识点的总结和各方面的素质培养也有帮助。
分析:我们可以构造图这样的几何图形,设正方形ABCD和正方形EFGH的边长分别为a、b。
则有[~公式~]
所以
[~公式~]
故[~公式~]
综上所述可证明平方差公式[~公式~]是恒成立的。当在讲解这个知识点给学生时,采用数形结合的思想将代数问题转化为几何问题,这样不仅让学生更能理解也能培养学生的数学基本能力。
2.求参数的值或参数的取值范围
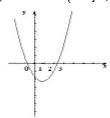
例2 若方程[~公式~]的两根满足:[~公式~],求[~公式~]的取值范围。
解析:画出与方程对应的二次函数 [~公式~]的草图:
由图可知:当[~公式~]时,[~公式~]; 当[~公式~]时,[~公式~]
即[~公式~];
[~公式~]
解得:[~公式~] 。
例3 若不等式组[~公式~]无解,则实数[~公式~]的取值范围是 ( )
A. [~公式~] B.[~公式~] C. [~公式~] D.[~公式~]
解: 若不等式组[~公式~]有解,则解得:[~公式~],`原不等式组的解集为[~公式~]。
把不等式组的解集在数轴上表示为:
若不等式组[~公式~]无解,则不等式组的解集在数轴上表示为:
也就是说-[~公式~]即可,则[~公式~].故选D。
小结:对于含参方程(不等式)可将其与图像联系起来,运用数形结合思想,去揭示问题中所蕴含的几何背景,往往能为解题提供清晰的思路。
3.求最值问题
例4 已知[~公式~]均为正数,且[~公式~]求[~公式~]的最小值。
解:如图,作线段AB=2,在AB上截取AE=[~公式~],EB=[~公式~],过A作AC⊥AB,且AC=2,过B作BD⊥AB,且BD=1。由勾股定理:CE=[~公式~],BD=[~公式~],原题即求CE+ED的最小值。
又如图,延长CA至G,使AG=AC,连接GE,由三角形两边之和大于第三边,则G、E、D三点共线时,GE+ED=DG最短。作出图形,延长DB至F,使BF//AG且BF=AG,连接GF。
则在Rt△DGF中,DF=1+2=3,GF=AB=2
`[~公式~]
`CE+DE的最小值是[~公式~]
即[~公式~]的最小值是[~公式~]。
小结:此题由式子特点联想勾股定理,构造图形解决问题。
4.用代数与三角方法解决几何问题
例5 如图,在△ABC中,AB>AC,CF、BE分别是AB、AC边上的高。试证:[~公式~]
证法一:(三角法)因为[~公式~],
`[~公式~]
`[~公式~]
`[~公式~]
(当[~公式~]时取等号)
证法二:(代数法)由AB>AC>CF,
AB>BE
及[~公式~]
`[~公式~]变形得: [~公式~]
`[~公式~]
`[~公式~]
当[~公式~]时,[~公式~]
综上:[~公式~]
数形结合是一种较为常见的数学教学方法,具有思路明确、形式简单、实用性强等特点。演绎推理和合情推理是数学命题教学常用的方法,也是数学问题解决的有效方法,对培养学生逻辑思维能力和创新意识具有重要的意义,在教学中应注意运用。在数学课堂逆向教学设计中运用数形结合的思想,遇到数与形问题时,能够学会怎样灵活逆向思考才更能达到捷径,从而达到事倍功半的效果;能够已知图形读出其中的数学信息或者已知题目中的数学文字信息能够转化为图形来解决问题,尽量摆脱对代数问题的抽象讨论,更多的是把有关代数里的知识用图形方式表示出来。因此,用逆向的思想结合数形结合的思想来解决问题相对来说要简单得多,有利于培养学生的数学思维能力。